数学基础知识

算法里涉及到一些数学常识，比如计算时间复杂度的时候，遇到$O(log N)$ 代表是什么意思？

搞清楚后需要简单记录，避免后忘记相关知识。

数学常识——对数

$log K$, 指的是对数k，百度百科定义如下：

在数学中，对数是对求幂的逆运算，正如除法是乘法的逆运算，反之亦然。 这意味着一个数字的对数是必须产生另一个固定数字（基数）的指数。

如果a的x次方等于N（a>0，且a≠1），那么数x叫做以a为底N的对数（logarithm），记作$x=log_aN$。其中，a叫做对数的底数，N叫做真数。

简单用公式来描述： $a^x=N$, 如果为了得出x的值，可以用表达式 $x=\log_aN$， a是对数的底数， N是真数， 通常我们定义当a=2的时候，忽略不写底数a，比如$2^x=N$，可以简写为 $log N$

还有一些其他对数简写：

• log以e为底，以x为真数， 可以写作：$log_ex = ln x$
• log以10位底，以x为真数， $log_{10}x =lg x$

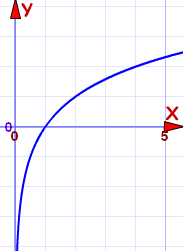
$log N$的曲线图如下：

数学常识——常数e

e代表是数学常数e, 是自然对数的底数 自然对数是以e为底的对数函数，e是一个无理数，约等于2.718281828

更加简单的说，假如你有1块钱，银行抽风了一年利率100%，如果一年结算一次，

• 一年后就能得到1×(1+1)=2块钱
• 如果半年结算一次，上半年的计息计入下半年的本金，一年后就能得到1×(1+0.5)×(1+0.5)=1×(1+0.5)=2.25块钱。这样就多出了两毛五。
• 如果像余额宝一样，每天都结算利息，那么一年后你就能得到 $1*(1+1/365)^365=2.7145674550$
• 比一年结算一次多了 七毛多
• 那么，如果每一秒结算一次，或者每一毫秒结算一次，或者每过无穷短的时间结算一次。那么钱岂不是可以一直加下去？x代表结算次数， 计算公式： ${lim_{x \to \infty} (1+1/x)^x}$

答案是否定，最终一年后我们能得到的钱最多只能是约等于2.71828182845904523536，也就是e。

综上，e的含义可以理解为增长的极限，“自然常数”的“自然”也可以理解为它是非人为的，我们只是发现了它。就像圆周率π一样，它也存在于生活的很多地方。